기본 알고리즘

알고리즘은 다음과 같이 정의할 수 있다.

문제를 해결하기 위한 것으로, 명확하게 정의되고 순서가 있는 유한개의 규칙으로 이루어진 집합

물론 명확하게 알고리즘을 정의해도, 변수의 값에 따라 결과가 맞기도하고 틀리기도 하면 올바른 알고리즘이라 할 수 없다. 따라서 다양한 변수값을 통해 알고리즘이 올바른지 확인하는 것도 중요하다.

 

 

기본적인 연습문제

---

최댓값, 최솟값

 

Q1. 세 값의 최댓값을 구하는 max3 메서드를 작성하시오

 

    public void max3(int a, int b, int c){
        int max = a;
        if(max<b) max = b;
        if(max<c) max = c;

        System.out.println("세 수 최댓값:"+max);
    }

    @Test
    public void max(){
        max3(1,4,6);
    }

 

 

Q2. 네 값의 최댓값을 구하는 max4 메서드를 작성하시오

 

    public void max4(int a, int b, int c, int d){
        int max = a;
        if(max<b) max = b;
        if(max<c) max = c;
        if(max<d) max = d;

        System.out.println("네 수 최댓값:"+max);
    }
    
    @Test
    public void max4(){
        max4(1,11,6,2);
    }

 

Q3. 세 값의 최솟값을 구하는 min3메서드를 작성하시오

 

 

    public void min3(int a, int b, int c){
        int min = a;
        if(min>b) min = b;
        if(min>c) min = c;
        
        System.out.println("세 수 최솟값:"+min);
    }
    
    @Test
    public void min3(){
        min3(6,22,3,15);
    }

 

Q4. 네 값의 최솟값을 구하는 min4 메서드를 작성하시오

 

    public void min4(int a, int b, int c, int d){
        int min = a;
        if(min>b) min = b;
        if(min>c) min = c;
        if(min>d) min = d;

        System.out.println("네 수 최솟값:"+min);
    }
    
    @Test
    public void min4(){
        min4(4,22,9,10);
    }

 

---

a,b,c 세 값의 대소 관계의 조합은 13가지가 있는데, 아래 그림은 그 조합을 나열한 것이다.

모양이 나무 형태이므로 결정트리 ( decision tree ) 라고 한다. 결정 트리는 왼쪽 끝(a>=b) 에서 시작해서 오른쪽으로 이동한다. 조건이 성립하면 윗가지로, 성립하지 않으면 아랫가지로 이동한다. 

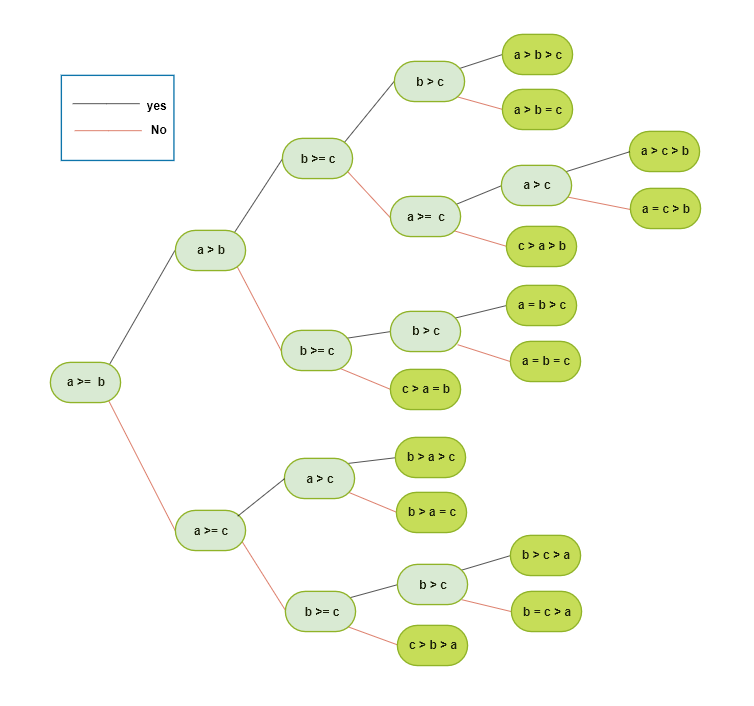
오른쪽 끝의 진한 녹색 안은 세 변수 a, b, c 의 대소 관계를 나타낸다.

---

세 값의 중앙값

최댓값, 최솟값과 달리 중앙값을 구하는 절차는 매우 복잡하다. 그래서 수많은 알고리즘을 생각할 수 있다.

세 값의 중앙값을 구하는 과정은 '퀵 정렬' 에서도 이용한다.

   public int med3(int a, int b, int c){
        if(a>=b)
            if(b>=c)
                return b;
            else if (a<=c)
                return a;
            else
                return c;

        else if (a>c)
            return a;
        else if (b>c)
            return c;
        else
            return b;
    }
    
    @Test
    public void med3(){
        int middle = med3(3,3,2);
        System.out.println("중앙값 :"+middle);
    }